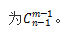“隔板模型”的特征是:n个相同元素分给m个不同对象,每个对象至少分一个元素,求所有可能的分法。“隔板模型”的解题思路是:将n个元素排成一排,在n个元素之间形成的n-1个间隙中放置m-1块隔板,即可把它隔成m份,这样所有不同的插入方法就是n个相同的元素分给m个不同对象的所有情况数,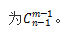
例1、共有10本完全相同的书分到4个班里,每个班至少要分到一本书,共有几种不同分法?
A.84
B.75
C.64
D.45
【解析】答案选A。先将10本相同的书排成一排,10本书之间出现了10-1=9个空隙,现在我们用4-1=3个挡板插入这9个空隙中,就把10本书隔成4份,正好分给4个班级;从9个空选3个插入3个相同挡板,不考虑顺序,按照公式计算出有84种。故正确答案为A。
例2、共有6本完全相同的书分到4个班里,共有多少种不同分法?
A.84
B.75
C.64
D.45
【解析】答案选A。由于会有不放书的班级,因此需要将问题转化为标准的隔板模型。先从每个班级借一本书,则现在有10本书,问题就转化为“将10本完全相同的书分给4个班,每班至少分到一本”。从10本书排成一排所形成的10-1=9个空隙里选择3个空隙插入隔板,就把10本书隔成4份,正好分给4个班级,每个班至少一本书,按照公式计算出有84种。则不同的分法故正确答案为A。
例3、共有14本完全相同的书分到4个班里,每个班至少分到两本书,共有多少种不同分法?
A.84
B.75
C.64
D.45
【解析】答案选A。由于每个班级至少分两本,因此需要将问题转化为标准的隔板模型。每个班级先发1本书,还剩10本,则问题转化为“将10本完全相同的书分给4个班,每班至少分到一本”。从10本书排成一排所形成的10-1=9个空隙里选择3个空隙插入隔板,就把10本书隔成4份,正好分给4个班级,按照公式计算出有84种。故正确答案为A。
通过上面三个例子对比,大家会发现虽然下面两个例子与“隔板法”题型特征不符,但是我们可以通过转换使其满足条件,最终还是可以借助公式来解题。希望同学们在平日的学习中能够多多练习,真正把所学方法内化于心,外化于行,做到信手拈来!