2021年浙江省考越来越近了,同学们是不是心里很慌!肯定会有很多同学觉得,会了的知识点现在却想不起来,不会的知识点还是不会......本文,
浙江公务员考试网小编给大家整理了行测常考知识点汇总。
1、选词填空技巧
相异语素定词义:
词语的适用对象/指代范围:
做客:接受别人的邀请或者主动去探访别人;欢迎来我们家做客。
作客:求学、谋生、创业等外在原因寄居他乡;作客他乡十载,虽说事业有成,却十分思念故土。
边界:“界”是界限,边界,两国间领土的界限。
边境:“境”是区域,边境,靠近边界的地方。
词义的轻重程度:
衰退、衰败:“退”是减弱,“败”是破败。后者显然语义较重。
违反、违犯:“反”指方向相背,“犯”是抵触。“违犯”比“违反”词义重。
词义的侧重点:
侵袭、侵蚀:袭,袭击;蚀,损耗。“侵袭”指侵入并袭击的行为,而“侵蚀”指侵害并使之受损。分别侧重过程和结果。
紧缺、紧俏:缺,缺乏;俏,指货物的销路好。“紧缺”指货物、资金或人员因短缺而紧张,“紧俏”指商品因销路好而供不应求。二词各侧重不同的角度。
色彩意义定风格:
褒义词(成果):肯定、喜爱 口头语(小气/老套):通俗 自然
贬义词(后果):否定、厌弃 书面语(吝啬/窠臼):文雅 庄重
中性词(结果):中立、客观
语体特征做排除:
公文通报:准确简明、浅显易懂,拒绝修辞化表达。
政论时评:逻辑严密、官方用语,适当形象化表达。
新闻报道:客观精炼、通俗时效,中性词运用较多。
科技说明:学术专业、客观分析,修辞手法不多见。
文艺作评:语言艺术、表达灵活,修辞手法较常见。
广告宣传:严谨得体、醒目生动,修辞运用较讲究。
2、片段阅读技巧
结合选项做排除
A. ③②⑥⑤④① B. ⑥①⑤④③②
C. ④①③②⑥⑤ D. ③②④①⑥⑤
首句④、⑥各出现一次,③出现两次;
尾句①、②各出现一次,⑤出现两次。
少数服从多数,D最有可能正确
A. ⑤②①⑥③④ B. ②④①⑥③⑤
C. ②⑥①④③⑤ D. ⑤⑥②③①④
将首尾句的筛选范围由四句缩小到两句,需要结合首句适用原则
A. ⑤②①⑥③④ B. ④②①⑥⑤③
C. ②⑥①④③⑤ D. ⑥⑤②③④①
首尾句没有规律,需要逐一排查,同时结合内部逻辑和关系
★首尾内容有讲究
首句不出现这些内容:
反面论证:否则、不然、如果没有,如果不
补充表述:当然、也、又
指示代词:这、这些、那、那些、此
结论总结:因此、所以、最终、终于
首句可以出现这些内容:
引用的别人的观点 背景性的陈述 设问提出话题
尾句一般出现这些内容
因此、因而、总之、可见、综上所述
★五大基础思维
1.代入排除:
代入排除思维是数量关系第一大法,优先考虑。
2.特值思维:
对于有些问题,若能根据其具体情况,合理巧妙地对某些元素赋值,特别是赋予确定的特殊值,往往能使问题获得简捷有效的解决。题干中有分数,比例,或者倍数关系时一般采用赋值法简化计算,赋值法经常应用在如工程问题,行程问题,费用问题等题目中。
3.倍数比例法:
若a : b=m : n(m、n互质),
则说明: a占m份,是m的倍数;
b占n份,是n的倍数;
a+b占m+n份,是m+n的倍数;
a-b占m-n份,是m-n的倍数。
4.奇偶特性法:
两个奇数之和/差为偶数,两个偶数之和/差为偶数,一奇一偶之和/差为奇数;
两个数的和差为奇数,则它们奇偶相反,两个数的和/差为偶数,则它们奇偶相同;
两个数的和为奇数,则其差也为奇数,两个数的和为偶数,则其差也为偶数
5.方程法:
很多数学运算题目都可以采用列方程进行求解。
方程法注意事项:未知数要便于列方程;未知数可以用字母表示,也可以用“份数”,还可以用汉字进行替代。
★五大模型
模型一:牛吃草模型
此模型是指存在一个定量,同时既有使其增加的量,也有使其减少的量,简单概括就是有进有出。这种题型常见的就是以排比句的形式出现,并且每一句话中都会出现两个数,一个表示数量,一个表示时间。
示例:牧场上有一片青草,每天都生长得一样快。这片青草供给N1头牛吃,可以吃t1天,或者供给N2头牛吃,可以吃t2天,如果供给N3头牛吃,可以吃几天?
对于这种题型核心公式:原有草量=(N1-X)×t1 =(N2-X)×t2=(N3-X)×t3
所以只需要根据题干的规律,用表示数量的数字-x的结果乘以对应的时间列出方程即可。
例题 牧场上有一片青草,每天都生长得一样快。这片青草供给10头牛吃,可以吃22天,或者供给16头牛吃,可以吃10天,如果供给27头牛吃,可以吃几天?
A、5 B、6 C、7 D、8
答案:A 分析:(10-x)×22=(16-x)×10=(27-x)×t3
解之得 X=5,t3=5天
常见形式:牛吃草、排队收银/检票、抽水放水、开采资源、爬自动扶梯等。
模型二:直线多次相遇问题
从两地同时出发的直线相遇问题中,第n次相遇时,路程和等于第一次相遇时路程和的2n-1倍,每个人走的路程等于他第一次相遇时所走路程的2n-1倍。
例题 甲乙两汽车同时分别从A、B两地相向而行,在离A 城52千米处相遇,到达对方城市后立即原速沿原路返回,在离A城44千米处相遇。两城市相距多少千米。
A、100 B、112 C、156 D、165
答案:B 第一次相遇时乙汽车走了52千米,根据直线多次相遇的规律,从开始到第二次相遇时乙汽车走了52*3=156千米,根据题意,两城市相距156-44=112千米。
模型三:错位重排问题
每一对元素都有一个一一对应关系,问打破每一对一一对应关系的方法数,此种方法叫做错位重排。
例题:实验室有三种不同的溶液,且都有对应的标签,问着三个瓶子标签贴错的情况有( )
A、1 B、2 C、9 D、6
答案:B,这个是三对元素的错位重排,故方法数有2种。
模型四:环形排列
N个人围成一圈,不同的排列方式有:
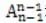
种。
例题 5个人手拉手围成一个圆圈,问共有多少种不同的方法?
A、120 B、24 C、60 D、30
答案:B。=24种。
模型五:多次独立重复试验
事件A发生的概率为P,连续进行n次,恰有k次发生的概率为
例题:运动员进行射击比赛,一共打了6枪,已知他每枪中10环的概率是0.7,求该运动员打中4次10环的概率为( )
A、22% B、32% C、40% D、45%
答案:B 所求概率为
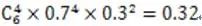
★图形推理规律
1.元素凌乱:题干中各图形元素凌乱,几乎没有相同点,优先考虑数量关系的考点,规律的出发点可以是:点、线、角、面、素。元素凌乱除了考查图形的数量关系外,还可能考的是图形的属性,即几何特征。
2.元素相同。题干图形中所包含的元素个数与种类相同,优先考虑图形的位置变化,包括图形中元素的平移、旋转以及翻转。
3.元素相似。题干各图形元素呈现相似的特征,在元素个数上可能存在差异,则可以考虑图形的样式遍历(缺什么补什么)、组合叠加(直接叠加、加减同异、黑白叠加)。
4.空间折叠。空间折叠题最重要的是分析图形的相邻面和相对面,可以通过移动的方式找准各面之间的关系,根据“相对面只能看到其中一个、相邻面看公共边”的特征选择正确答案
★判断推理规律
翻译推理
三个基本定理
逆否定理:A推出B→否B推出否A
肯前肯后,否后否前
摩根定律1:否(A或B)→否A且否B
摩根定律2:否(A且B)→否A或否B
七条基本翻译
所有(凡是)S都是P,S推出P
所有(凡是)S不是P,S推出非P
没有S是P,p推出非S
不是S都不是P,P推出S
充分条件:P推出Q。如果P,那么Q;只要P,就Q;凡是P,都Q
必要条件:Q推出P。只有P,才Q;除非P,否则不Q;P是Q必不可少的条件。
排中律:非P即Q,非Q即P。或者P,或者Q;要么P,要么Q
★三种基本关系
矛盾关系
矛盾是指两命题非此即彼的关系,两命题的真假情况必定为“一真一假”。
反对关系
上反对关系:全称肯定命题与全程否定命题。可同假,不可同真。
下反对关系,特称肯定命题与特称否定命题。可同真,不可同假。
包容关系
包容是指,若A真,则B也真,即有:A→B。两个命题,若命题中只有一真,则A必为假;若命题中只有一假,则B必为真。“一真前假,一假后真”
★逻辑论证
1. 加强论证
(1)非因果类:
①增强论点(通过解释、重申论点进行加强)
②增强论据:分为两种,一种是补充一个正面论据,另一种是解释原有的论据,二者均可起到加强作用
③从论证方式入手:搭桥(将论点与论据联系起来,往往既包含论据的关键词又包含论点的关键词。)和补充前提(这是论点得以成立的必要条件/基础,可以用否定代入法进行验证)。
(2)因果类:①排除他因—排除其他导致结果出现的原因;②对比实验—有A有B,没A没B。
考试过程中,当出现多个加强选项时,注意加强强度的比较:加强论证方式(搭桥)>加强论点>加强论据。而对于选择前提的题目来说,直接就题目设问方式选择前提。
2. 削弱论证
(1)非因果类:①削弱论点;②削弱论据;③削弱论证方式(拆桥);④否定前提。
(2)因果类:①另有他因—还有其他原因导致结果的出现;②对比实验—有A无B,无A有B;③因果倒置。
考试过程中,当出现多个削弱选项时,注意削弱强度的比较:削弱论点>削弱论证方式(拆桥)>削弱论据。而因果类中削弱强度,因果倒置最强,因为因果倒置推翻了原有的因果关系,重新建立了新的因果关系,是从本质上否定了。




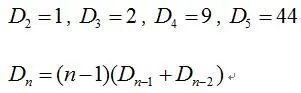
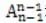 种。
种。

.jpg)
